Prismas
Questão 1:Em um prisma regular triangular, cada aresta lateral mede 10 cm e cada aresta da base mede 6 cm. Calcular desse Prisma:
a) a área de uma face lateral.
b) a área de uma base.
c) a área lateral.
d) a área total.
Resolução:a) Af = (6.10) cm²
Af = 60 cm²
b) Cada base é um triângulo equilátero de lado 6 cm. Lembrando que a altura
h de um triângulo equilátero de lado a é dada por

Portanto, a área B de uma base é:
c) A área lateral AL é a soma das áreas das três fases laterais, isto é:
AL = 3 . Af
AL = 3 . 60 cm²
AL = 180 cm²
d) A área total At é a soma da área lateral AL com duas vezes a área B de uma base, isto é:
At = AL + 2B
At = (180 + 18 √3) cm²
Questão 2:Um prisma reto de altura 10 cm tem como polígonos das bases triângulos retângulos de catetos 3 cm e 4 cm. Calcule a área total desse prima.
Resolução:
Questão 3:Em uma piscina regular hexagonal cada aresta lateral mede 8 dm e cada aresta da base mede 4 dm. Calcule, desses prisma:
a) a área de cada face lateral;
b) a área de uma base;
c) a área lateral;
d) a área total;
Resolução:a) Af = b . h
Af = 4 .8
Af = 32 dm²
b) Ab = (6.10 √3) / 4
Ab = 24 √3 dm²
c) AL = 6.4.8
AL = 192 dm²
d) At = 2.24 √3 +192
At = 48 √3 + 192 dm²
Diagonais do Paralelepípedo Questão 1:As dimensões de um paralelepípedo reto-retângular são 20 cm, 12 cm e 9 cm.Calcular a medida de uma diagonal desse paralelepípedo.
Resolução:D = √a² + b² + c²
D = √20² + 12² + 9²
D = √400 + 144 + 81
D = √625
D = 25 cm²
Questão 2:O comprimento EA, a largura EH e a altura EF do paralelepípedo reto-retângulo representado ao lado são 12 cm, 3 cm e 4cm, respectivamente:
Calcule:
a) a medida de uma diagonal da face EFGH;
b) a medida de uma diagonal do paralelepípedo;
c) a área total do paralelepípedo;
d) o volume do paralelepípedo;
Resolução:a) D = √3²+4²
D
= √9 + 16
D = √25
D = 5 cm²
b) D = √3² + 4² + 12²
D = √9 + 16 + 144
D = √169
D = 13 cm²
c) A1 = 12 . 3 A2 = 4.3 At = A1 + A2
A1 = 36 A2 = 12 At = 144 + 24
A1 = 4.36 A2 = 2.12 At = 168 cm²
A1 = 144 A2 = 24
d) V = b.h.l
V = 12.3.4
V = 169 cm³
Cubo Questão 1A área total de um cubo é 54 cm². Calcule a medida da diagonal desse cubo.
Resolução:Ac = 6a² dc = a√3
54 = 6a² dc = 3√3cm²
54 /6 = a²
a = √9
a =3 cm
Questão 2A diagonal
de um mede √75 cm .Calcule a área total desse cubo:
Resolução:d = √75
d = L√3
√75 = L√3
5√3 = L√3
L = (5√3) / √3
L = 5 cm
Questão 3:
Se a soma das medidas de todas as arestas de um cubo é 60 cm,então o volume desse cubo, em centímentros cúbicos, é:
a) 125 cm³
b) 100 cm³
c) 75 cm³
d) 60 cm³
e) 25 cm³
Resolução:12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
Letra a) 125 cm³











.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)













.jpg)
.jpg)
 o raio. A área total de um círculo é
o raio. A área total de um círculo é  . A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e
. A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e  , já que a área do sector é diretamente proporcional ao ângulo:
, já que a área do sector é diretamente proporcional ao ângulo:
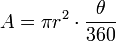
 , do arco de um sector é dado pela seguinte fórmula:
, do arco de um sector é dado pela seguinte fórmula: