POLIEDROS
Os poliedros são figuras geométricas formadas por vértices, arestas e faces. Através da expressão de Euler, é possível determinar o número de vértices, arestas e faces dos poliedros.
As figuras geométricas espaciais também recebem o nome de sólidos geométricos, que são divididos em: poliedros e corpos redondos. Vamos abordar as definições e propriedades dos poliedros.
Poliedros são figuras geométricas formadas por três elementos básicos: vértices, arestas e faces. Um poliedro é considerado regular quando suas faces são polígonos regulares e congruentes.
.jpg) Dentre os poliedros existentes, existem alguns considerados Poliedros de Platão, pois todas as faces possuem o mesmo número de arestas, todos os ângulos poliédricos possuem o mesmo número de arestas e se enquadram na relação de Euler. Os Poliedros considerados de Platão são:
Dentre os poliedros existentes, existem alguns considerados Poliedros de Platão, pois todas as faces possuem o mesmo número de arestas, todos os ângulos poliédricos possuem o mesmo número de arestas e se enquadram na relação de Euler. Os Poliedros considerados de Platão são:
.jpg) Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.
A fórmula de Euler está atribuída à relação de dependência entre os elementos de um poliedro. A expressão matemática desenvolvida por Leonhard Euler, matemático suíço, é a seguinte: V – A + F = 2. Onde:
V = vértice
A = arestas
F = Faces
Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.
A fórmula de Euler está atribuída à relação de dependência entre os elementos de um poliedro. A expressão matemática desenvolvida por Leonhard Euler, matemático suíço, é a seguinte: V – A + F = 2. Onde:
V = vértice
A = arestas
F = Faces
Essa expressão determina o número de faces, arestas e vértices de qualquer poliedro.
Por volta do século VI antes de Cristo, o filósofo Platão estudou os poliedros platônicos relacionando-os aos elementos da natureza. Veja a associação feita por ele:
Tetraedro: fogo
Hexaedro (cubo): terra
Octaedro: ar
Icosaedro: água
Dodecaedro: universo
Além dos poliedros de Platão, os sólidos geométricos como: prismas, pirâmides, paralelepípedos, blocos retangulares e quadrangulares são considerados poliedros.
.jpg)
.jpg)
Setor circular
Um sector circular ou sector de círculo, também conhecido comofatia de pizza, é a parte de um círculo limitada por dois raios e umarco. Dependendo do valor de seu ângulo central, um setor pode ser classificado como metades (180º), quadrantes (90º) e oitantes (45º).1Cálculo da área em função do ângulo central
Seja θ o ângulo central, em radianos, e  o raio. A área total de um círculo é
o raio. A área total de um círculo é  . A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e
. A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e  , já que a área do sector é diretamente proporcional ao ângulo:
, já que a área do sector é diretamente proporcional ao ângulo:
 o raio. A área total de um círculo é
o raio. A área total de um círculo é  . A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e
. A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e  , já que a área do sector é diretamente proporcional ao ângulo:
, já que a área do sector é diretamente proporcional ao ângulo:
Também, se θ refere-se ao ângulo central em graus, uma fórmula similar pode ser derivada:
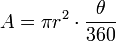
Cálculo da área em função do comprimento do arco
- O comprimento,
 , do arco de um sector é dado pela seguinte fórmula:onde θ está em graus. Quando θ estiver em radianos, a fórmula anterior pode ser reescrita comoDessa forma, substituindo o valor de L encontrado acima na fórmula para o cálculo da área, podemos obter a área do setor circular em função de tal comprimento, conforme a seguinte equação:
, do arco de um sector é dado pela seguinte fórmula:onde θ está em graus. Quando θ estiver em radianos, a fórmula anterior pode ser reescrita comoDessa forma, substituindo o valor de L encontrado acima na fórmula para o cálculo da área, podemos obter a área do setor circular em função de tal comprimento, conforme a seguinte equação:
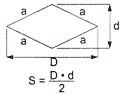
- Área das figuras planas
Retângulo Quadrado Triângulo Paralelogramo Trapézio Losango Triângulo equilátero Como calcular área do círculo e do setor circular – Fórmula da área
Calcular a área de um círculo e do setor circular é muito pedido em diversos exercícios e nas diversas provas de vestibulares pelo país.Área do círculoA fórmula para calcular a área do círculo é a seguinte: A = πr2 .O “r” significa raio e pode ser calculado dividindo o valor do diâmetro por dois. Ou seja, o raio é a metade do diâmetro.Área do setor circularSe o ângulo central for dado em radianos a fórmula para calcular a área do setor circular será:Se o ângulo central for dado em graus a fórmula para calcular a área do setor circular será:Se for dado r e l a fórmula para calcular a área do setor circular será:Na figura abaixo o “α” representa o ângulo, o “r” o raio e o “l” o comprimento do arco do setor circular. A parte riscada de azul da figura representa a área do setor circular.







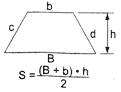




Nenhum comentário:
Postar um comentário