Poliedro
Os poliedros são figuras que fazem parte da geometria espacial, ou seja,
possuem três dimensões (comprimento, largura e altura), formados
de vértices, arestas e faces. As faces do poliedro são formadas
por polígonos (figura plana composta de n lados) e as arestas e os vértices
correspondem aos lados e aos vértices dos polígonos.
Teorema de Euler
O Teorema ou Relação de Euler é válido somente para poliedros regulares, os
quais todas as faces possuem o mesmo número de arestas e são compostos
de polígonos regulares, ou seja, cada um com o mesmo número de lados.
Ademais, nos polígonos regulares, para cada vértice, converge um mesmo
número de arestas. Não obstante, o Teorema de Euler estabelece uma relação
entre o número de faces, vértices e
F + V = 2 + A ou V - A + F = 2
F: número de faces
V: número de vértices
A: número de arestas
Classificação dos Poliedros
Os poliedros são classificados em regulares e não regulares. Dessa forma, os
poliedros regulares surgem quando suas faces formam polígonos regulares e
congruentes; por sua vez, os poliedros não regulares são formados por
polígonos regulares e irregulares.
Poliedros Regulares
Os poliedros regulares convexos são formados pelos cinco “Sólidos Platônicos”
ou “Poliedros de Platão”, a saber: tetraedro, hexaedro (cubo), octaedro,
dodecaedro, icosaedro.
Definição de não-poliedros
Não-poliedros são sólidos geométricos que têm pelo menos uma superfície
curva (cone, cilindro, esfera e outros).
Elementos de não-poliedros
Um não-poliedro pode ser constituído apenas por uma superfície curva (esfera)
ou pode apresentar também superfícies planas. Depende do não-poliedro
poderá ter bases e vértices.
https://www.youtube.com/watch?v=w4Bx0S9P1wA
.jpg)
.jpg)
 o raio. A área total de um círculo é
o raio. A área total de um círculo é  . A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e
. A área do sector pode ser obtida multiplicando-se a área total do círculo pela razão entre θ e  , já que a área do sector é diretamente proporcional ao ângulo:
, já que a área do sector é diretamente proporcional ao ângulo:
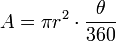
 , do arco de um sector é dado pela seguinte fórmula:
, do arco de um sector é dado pela seguinte fórmula: